Atlas of Tonespace
by monxmood
Theories of tuning are generally based on the harmonic series, which is the sequence of component sine waves present in complex musical sounds such as the vibration of a violin string. The harmonic series of a fundamental frequency "f" is simply its multiples. The musical intervals between these sinewaves can be expressed as fractions of one sinewave over another. So the interval between the fourth and fifth sinewave (a major third) can be written as 5f over 4f, which, cancelling out the f's, gives 5/4. As a general rule, in most sounds, the higher the harmonic the less perceptible it is. So it follows that fractional relationships between frequencies also become harder to recognize, the higher the numbers involved.
It is useful to distinguish between the idea of a Tone Factory, which can generate a limited or unlimited number of frequencies, and the Tone Set, which is the ensemble of those frequencies considered useful in a given culture.
The Chinese One-Dimensional Tone Factory
The Chinese and Pythagoras both knew about the fifth, which is 3/2 times the frequency of the root note. They both discovered that if you stack 12 fifths you arrive at a note pretty close to seven octaves higher than the note you started on. The error was called the Pythagorean comma, and the Chinese may have had a name for it as well. It can be expressed as a a fraction: 531441/524288; as a percentage: 1.36%; or in cents (hundredths of a semitone): 23.46 cents.
Equal Temperament
Equal Temperament wasn't invented by Bach but he brought it to fruition. It works by dividing the Pythagorean comma into twelve equal parts called schismas (meaning "a division", one schisma = 1.955 cents) and adding one to each fifth so that they meet up neatly at the top of the stack of twelve. The same effect can be obtained by defining each semitone rise as an increase in frequency by the twelfth root of two.
the 31-notename system
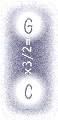
Such a system of tuning could have brought about a wonderful simplification of notation, not to mention the possibility of simplified keyboards, but we were not to be so lucky. Thanks to rearguard action from the inevitable diehards, antique distinctions of tuning were preserved in the notation, resulting in a system of 31 names for 12 tones. If the sole system of natural tuning were the Chinese/Pythagorean system of stacked fifths, a case could be made for keeping these 31 (or even more) names, on the grounds that they refer unequivocally to specific products of the Chinese Tone Factory.
But, as you are about to see, it is not the only system of tuning, nor is it the only system for deciding on notenames. The "thirds" spelling rule, which states that triads, including diminished and augmented, must be spelled with alternating letters, comes into direct conflict with the 31 note ladder system and renders the whole sharp/flat system so ambiguous as to be useless.
The Indian Two-Dimensional Tone Factory
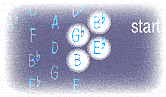
So let's have a look at the so-called just system of tuning, originally from India and named after a Greek called Aristogenes or Aristoxenos. Instead of relying solely on the fifth (3/2), it introduces thirds, both major (5/4) and minor (6/5) into the picture, forming a web of frequency relationships which I have organised as a honeycomb. Note that however far we extend this honeycomb in any direction, we will never find two notes of exactly the same frequency!

The Indians and Aristoxenos had a comma too, called the syntonic comma, which as a fraction is 81/80; as a percentage: 1.25%; and in cents: 21.51. This comma was considered the smallest nuance distinguishable by the human ear. In Indian music it is the distance between two neighbouring shrutis. Here, each plus or minus represents a difference of one comma.

Aristoxenos versus E.T.
We should take this opportunity to zoom out and see how all the honeycomb frequencies compare to Equal Temperament - the MIDI standard. The E.T. semitone or halftone is divided into 100 cents, which are the same as those displayed on your electronic tuner.

A note sitting on the bold line going down the middle is in tune to E.T. Notes on the left are sharp and those on the right are flat. The pale lines represent cents. If you click on one of the lower rows you will see a dotted line joining two notes only 1.954 cents apart, almost the same value as the Pythagorean schisma (see above). It fulfills a similar function, because being imperceptible to all but the gods, both the Turkish and the Indians (and maybe others) have used it to simplify and limit their tone factory output. You can liken it to a warp or wormhole in tonespace forming a shortcut between two distant points. So I don't know whether to call it the Oriental wormhole, or Turkish Tonewarp.
In this chart I have given the notes names according to the "thirds" rule. You can see by running your mouse over a few names that the same name may represent several widely differing frequencies, while two notes joined by the dotted line will have different spelling. Enharmonic spelling, a legacy of the Pythagorean system, breaks down completely with Just Tuning.
The Indian Shruti Set
By taking 5 complete sets of 12 notes one syntonic comma apart we get the Indian tone factory arranged in five interlocking tiles

We can identify each tile/chromatic set by +'s and -'s relative to the middle set. Each plus or minus represents a difference of one comma. (If you are puzzled by the positions of the red and blue tiles, check out that wormhole again.) Indian musicians recognise these differences by listening for the emotion they carry. Without going into details here I have marked the emotional categories by colouring the tiles blue, green, white, yellow and red.
However since Indian music is played against a continuous drone (which we will call C) some substitutions have been made to create the Master Shruti Set in order to avoid having tones that are simply too far away from C. Note that some tones from the red series have crossed over the quartertone divide to the blue series and vice versa.

Debussy and Three-Dimensional Tonespace
We have seen how the Chinese/Pythagorean system uses one prime number - 3 - to build a one-dimensional (linear) space: the stack of fifths; and how the Indian/Aristoxenian system uses two prime numbers - 3 & 5 - to build a two-dimensional space: the honeycomb. (I realise that 2 is also a prime, but as I said at the beginning, all powers of 2 including 1 - zero power - are interchangeable here. We are just using them as a lubricant to help us compare frequencies in the same octave.) What we find is that each additional prime we introduce is accompanied by a new dimension.

Let's look at what happens when we add the prime number 7. We can create another honeycomb based on the numbers 5 and 7 on a plane which intersects our original honeycomb (as in the image above) along any 5_4 axis (i.e. any axis containing augmented chords, eg. c - e - ab). As you will see in the next chart, we get one whole tone set. It contains axes based on tritones, minor sevenths, and the augmented chords that were on the intersecting axis. If we follow two tritones to see the kind of octave they make we observe quite heavy error: 25/49, roughly 2%, or a third of a halftone. Here the grey lines represent 10 cents error vis a vis ET. Plus is to the left, minus to the right.

It was Debussy who introduced this extra plane - based on 7f and 5f - into Western music. In order to understand how such a feat can be achieved with a piano tuned to ET intervals, we will need to grasp tone token theory.
Tone Token Theory
This theory enables us to discover strategies for creating music out of unmusical intervals. Let us take the view that ET intervals are standing in for honeycomb intervals, in the same way that words like love, happiness, anger, sadness, etc. have to do duty for a wide range of subtle shades of those emotions. We can call this hypothesis "HH1":
HH1: The 12 notes of the ET set are tokens used to substitute for and denote natural tones drawn from an unbounded set situated on a honeycomb of several dimensions.
Can such a crude tool when set in the right hands recreate those subtleties? And, using the honeycomb, can we learn how it is done?
Let us look at some of the applications of all this in harmony and composing. I keep a stock of photocopies of the honeycomb on which I like to turn chords and scales into pretty patterns. You know: draw lines round the notes in a chord to make triangles, lozenges, parallelograms. In doing this I am testing hypothesis "HH2":
HH2: A harmonic chord is one whose tones are adjacent on the honeycomb (and therefore are related by simple fractions.) An ET chord written for (a good) choir or string orchestra will by default cause a harmonic chord to be played, and can therefore be said to be a token for that chord even when performed on an ET synthesizer.
Mainly, the honeycomb helps me see which notes are family rather than just neighbours. I can see (for example) that stationary, placid chords tend to fit into a maximum of two adjacent vertical columns. More exciting chords tend to spread out sideways. The tonic of any group is usually the bottom note in the shape. Chords with two bottom notes often sound curious.
HH3: A descending order of harmonicity exists which removes most of ET's ambiguities. A chord which can be traced on the 3f_5f honeycomb counts as more harmonic than a chord derived from the higher multiples of f.
And further, by making other honeycombs, I can get a picture of how many dimensions a chord is in. Some chords (a 4 2 4 2 for example) refuse to fit inside a single bubble on the 3f_5f honeycomb yet are elemental in the 5f_7f honeycomb.
HH4: Tones which are not adjacent to the nucleus of the chord on the 3f_5f honeycomb do not belong to that honeycomb at all, but belong to other dimensions (7f, 11f, 13f etc) and their intersections; the criterion being the lowest dimension wherein they can be found adjacent to the chord nucleus. (See the next section)
If I get an unusual scale I can draw it out on the honeycomb and see at a glance all the types of chords that could go with it. But I am careful about using it to generate composing ideas. For the moment I prefer to let the ideas come naturally and then trace them out on the honeycomb to see if there is some hidden symmetry. I expect to spend years seeing what sort of theorems it throws up, before putting any of them into practice.
The Eleventh Sinewave and Quarter Tone Composing
Despite the wide errors in the 7_5 honeycomb plane, a range of ET chords will serve as tokens to evoke that plane unambiguously. The main requirement is that they contain only notes belonging to one whole tone scale, such as seventh or ninth flatted five chords. If we wish to introduce the eleventh harmonic however, the 12 tone ET system has simply not enough resolution to do the job. The problem is that the 11th harmonic is 48 cents flat to ET, nearly a full quartertone. The trick usually used to indicate the 11f harmonic of say C is to have an A (as 6th or 13th) somewhere in the chord. This links the C to the blue F#-- in the shruti table, which would cause the first violins to play the note slightly flat, and get a bit closer to the desired frequency. The limitation of this system is obvious: we are obliged to have a four or more part root position chord to simulate the fourth dimension.The alternative, which is gaining ever wider acceptance among composers, is to attack the resolution problem by composing in quartertones.
Why can't we just use natural tuning?
Because of drift. Watch what happens if we use Just Tuning on a chord sequence like Giant Steps (by John Coltrane). Assuming that at least one common note is held from each chord to the next one, you will see that the tuning drifts downwards by nearly six commas (well over a halftone) per cycle. This kind of chord sequence is just not safe with unaccompanied choir, unless the singers have perfect pitch.
So are we doomed to suffer the crude ET system if we want harmony? Not necessarily. It is no longer beyond the bounds of human ingenuity to write realtime Just Tuning programs with microtone portamento to correct drift imperceptibly and give us the best of both worlds on a synthesiser. I have used the honeycomb to create chord analysis routines which I will send to anyone who wants to write the code.